터널 효과

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 한국에서의 연구 및 개발
3. 이론적 배경
- 3.1. 슈뢰딩거 방정식
- 3.2. WKB 근사
4. 응용 분야
5. 관련 현상
6. 더 알아보기
참조

1. 개요

터널 효과는 양자역학적 현상으로, 입자가 고전적으로는 통과할 수 없는 에너지 장벽을 낮은 확률로 통과하는 현상을 말한다. 1927년 프리드리히 훈트가 분자 이성질체 전이를 설명하기 위해 처음 도입했으며, 조지 가모프, 로널드 거니, 에드워드 콘던은 알파 붕괴를 통해 터널 효과의 실재를 증명했다. 이후 에사키 레오나는 반도체에서 전자의 터널링 현상을 발견하고, 기에버는 초전도체에서도 터널링이 일어남을 실험적으로 증명했으며, 조셉슨은 초전도 쿠퍼쌍의 터널링을 예측했다. 비닝과 로러는 주사 터널링 현미경(STM)을 개발하여 노벨 물리학상을 수상했다.

터널 효과는 양자역학의 중요한 개념으로, 입자를 파동으로 간주하여 퍼텐셜 장벽을 파동의 일부가 통과하는 것으로 설명한다. 슈뢰딩거 방정식과 WKB 근사를 통해 터널링 확률을 계산할 수 있으며, 장벽의 높이와 너비에 따라 터널링 확률이 달라진다.

터널 효과는 반도체 소자, 플래시 메모리, 터널 다이오드, 핵융합, 방사성 붕괴, 양자 생물학 등 다양한 분야에 응용된다. 특히 STM은 물질 표면의 원자 수준 구조를 관찰하는 데 활용되며, 핵융합에서는 쿨롱 장벽을 넘어 핵융합 반응을 일으키는 데 기여한다. 또한 DNA 돌연변이와 같은 생명 현상에도 영향을 미친다.

더 읽어볼만한 페이지

물리학 사이드바 - 파울리 배타 원리
파울리 배타 원리는 1925년 볼프강 파울리가 제시한 양자역학 원리로, 동일한 페르미온은 동일한 양자 상태에 존재할 수 없으며, 원자의 전자 배치, 화학 결합, 천체 특성 등을 설명하는 데 중요한 역할을 한다.
물리학 사이드바 - 양자역학
양자역학은 20세기 초에 개발된 물리학 이론으로, 미시적인 계의 성질과 거동을 설명하며, 불확정성 원리, 파동-입자 이중성 등의 개념을 포함하고, 현대 기술과 현대 물리학에 중요한 영향을 미친다.
역학 - 파울리 배타 원리
파울리 배타 원리는 1925년 볼프강 파울리가 제시한 양자역학 원리로, 동일한 페르미온은 동일한 양자 상태에 존재할 수 없으며, 원자의 전자 배치, 화학 결합, 천체 특성 등을 설명하는 데 중요한 역할을 한다.
역학 - 양자역학
양자역학은 20세기 초에 개발된 물리학 이론으로, 미시적인 계의 성질과 거동을 설명하며, 불확정성 원리, 파동-입자 이중성 등의 개념을 포함하고, 현대 기술과 현대 물리학에 중요한 영향을 미친다.
입자물리학 - 전자볼트
전자볼트는 전자가 1볼트의 전위차를 통과할 때 얻거나 잃는 에너지 단위로, 1.602 × 10⁻¹⁹ 줄과 같으며, 다양한 물리학 분야와 공학에서 에너지, 질량, 운동량, 온도, 거리 등을 표현하는 데 널리 활용된다.
입자물리학 - 알파 붕괴
알파 붕괴는 원자핵이 헬륨-4 원자핵인 알파 입자를 방출하여 원자 번호와 질량수가 감소하는 방사성 붕괴의 한 형태로, 무거운 원자핵에서 주로 발생하며 양자 터널링 효과로 설명되고 연기 감지기 등에 활용되지만 인체에 유해할 수도 있다.

터널 효과
구글 지도
기본 정보
현상 이름	양자 터널링
로마자 표기	yangja teoneolling
다른 이름	터널 효과
설명
정의	양자 역학에서 입자가 고전적인 역학에서는 통과할 수 없는 에너지 장벽을 통과하는 현상 전자가 에너지 장벽을 뚫고 이동하는 현상
비고	고전적인 역학에서는 불가능하지만, 양자 역학의 고유한 특성 때문에 발생함.
특징
확률	터널링은 절대적인 것이 아니라, 일정 확률로 일어남 입자가 장벽을 통과할 확률은 장벽의 높이와 폭에 따라 지수 함수적으로 감소
에너지	입자는 고전적인 역학에서 요구되는 에너지 없이도 장벽을 통과 가능
입자 종류	모든 종류의 입자(전자, 원자, 분자 등)에서 발생 가능
발견 및 역사
최초 발견	1927년, 프리드리히 훈트가 이중 바닥 포텐셜을 가진 분자의 기저 상태를 연구하면서 처음으로 발견 1928년, 조지 가모프, 로널드 거니, 에드워드 콘돈이 알파 붕괴를 설명하기 위해 이론적으로 제시함
주요 연구자	프리드리히 훈트 조지 가모프 로널드 거니 에드워드 콘돈
응용 분야
전자 기기	터널 다이오드, 터널 트랜지스터와 같은 양자 장치의 작동 원리 스캐닝 터널링 현미경(STM)과 같은 분석 장비에 활용 반도체 소자의 설계 및 제작에 중요 7/5 나노미터 이하의 반도체 공정에서 중요
핵물리학	알파 붕괴와 같은 핵반응의 메커니즘 설명 핵융합 반응에서 중요한 역할 수행
화학	화학 반응 속도 및 메커니즘 연구에 활용
기타	DNA 돌연변이 등 생화학적 과정에서 발생 가능 양자 컴퓨터 개발에 응용 가능성 연구 중
이론적 설명
슈뢰딩거 방정식	입자의 파동성을 기술하는 양자역학의 기본 방정식
파동 함수	입자의 존재 확률을 나타내는 함수, 장벽을 통과하면서 감쇠
에너지 장벽	입자가 통과해야 하는 포텐셜 에너지 영역
투과 계수	입자가 장벽을 통과할 확률을 나타내는 값
관련 개념
양자 역학	미시 세계의 현상을 설명하는 물리학 이론
파동-입자 이중성	입자가 파동의 성질과 입자의 성질을 동시에 갖는다는 개념
불확정성 원리	입자의 위치와 운동량을 동시에 정확하게 측정할 수 없다는 원리

2. 역사

1927년 독일의 프리드리히 훈트가 분자의 이성질체 사이의 전이를 다루기 위해 양자 터널링을 처음 도입하였다.^[100] 1928년 조지 가모프와^[101]^[102] 로널드 거니(Ronald W. Gurney), 에드워드 콘던(Edward U. Condon)이^[103] 터널 효과를 통해 알파 붕괴를 설명하여 터널 효과가 실재함을 증명하였다.^[12]^[13]^[14]^[15] 이들은 핵 퍼텐셜을 모델화한 슈뢰딩거 방정식을 풀고, 입자의 반감기와 방출되는 에너지와의 관계식이 터널 효과가 일어날 확률과 직접적인 관련이 있음을 밝혀냈다.^[58]^[59]^[60]^[61] 막스 보른은 가모프의 세미나에 참석한 후 터널 효과가 원자핵물리학뿐만 아니라 더 보편적인 현상임을 인식했다.^[62]

1957년 에사키 레오나는 반도체에서 전자의 터널링 현상을 발견하고 터널 다이오드를 개발했다.^[17] 1960년 아이버 기에버는 터널링이 초전도체에서도 일어난다는 것을 실험적으로 증명했다. 1962년 브라이언 조셉슨은 초전도 쿠퍼쌍의 터널링을 예측했다. 에사키, 기에버, 조셉슨은 고체에서의 양자 터널링에 대한 연구로 1973년 노벨 물리학상을 공동 수상했다.^[18]^[7]

1981년 게르트 비닝과 하인리히 로러는 양자 터널링 현상을 이용한 주사 터널링 현미경(STM)을 개발하여 1986년 노벨 물리학상을 수상했다.^[19]

2016년에는 물의 양자 터널링(Quantum tunneling of water)이 발견되었다.^[64]

2. 1. 한국에서의 연구 및 개발

3. 이론적 배경

주사터널링현미경(STM)에 대한 터널 효과와 그 응용을 보여주는 애니메이션

양자 터널링은 양자역학의 영역에 속한다. 퍼텐셜 장벽을 통과하려는 입자를 언덕을 넘으려는 공에 비유할 수 있다. 양자역학과 고전역학은 이러한 시나리오를 다루는 방식에서 차이가 있다.

고전역학은 장벽을 고전적으로 넘을 만큼 충분한 에너지를 갖지 못한 입자는 반대쪽에 도달할 수 없다고 예측한다. 따라서 언덕을 넘을 만큼 충분한 에너지를 갖지 못한 공은 다시 굴러 내려올 것이다. 양자역학에서는 입자가 작은 확률로 반대편으로 ''터널링''하여 장벽을 통과할 수 있다. 이러한 차이의 이유는 물질을 파동과 입자의 성질을 가진 것으로 다루기 때문이다.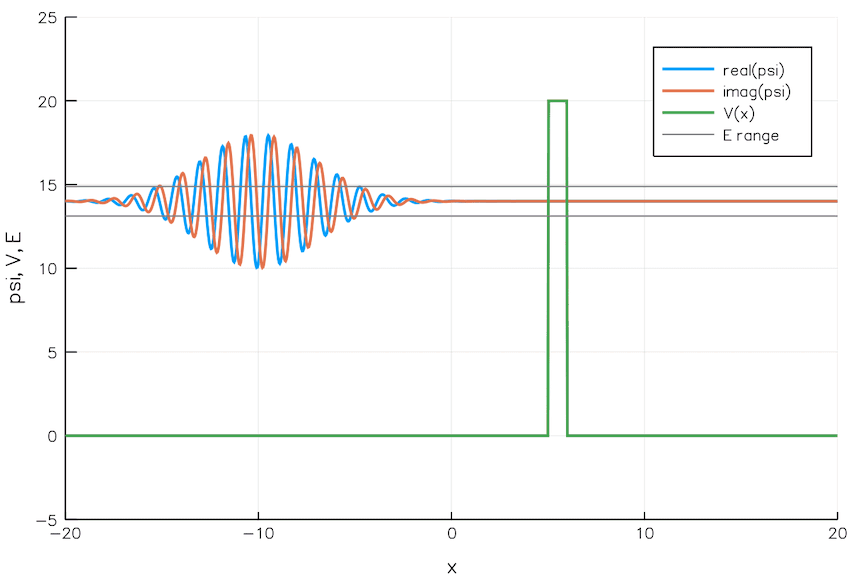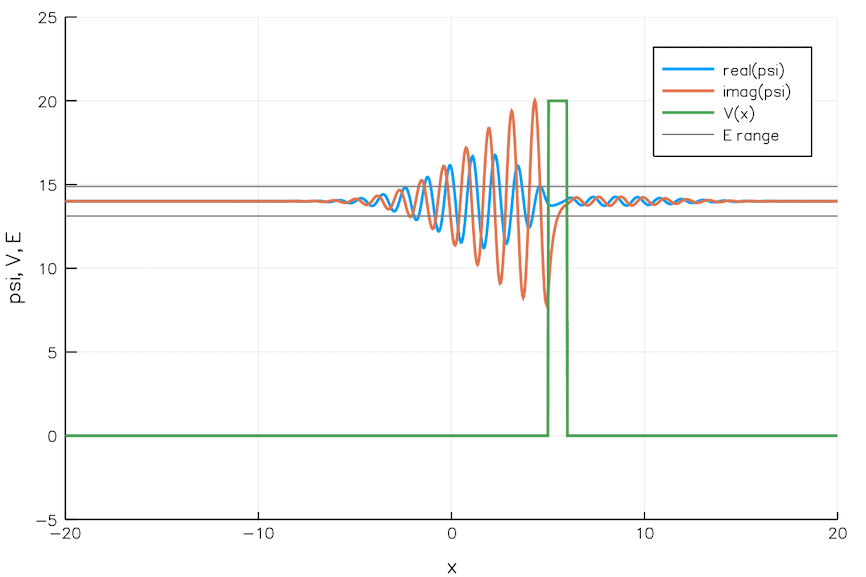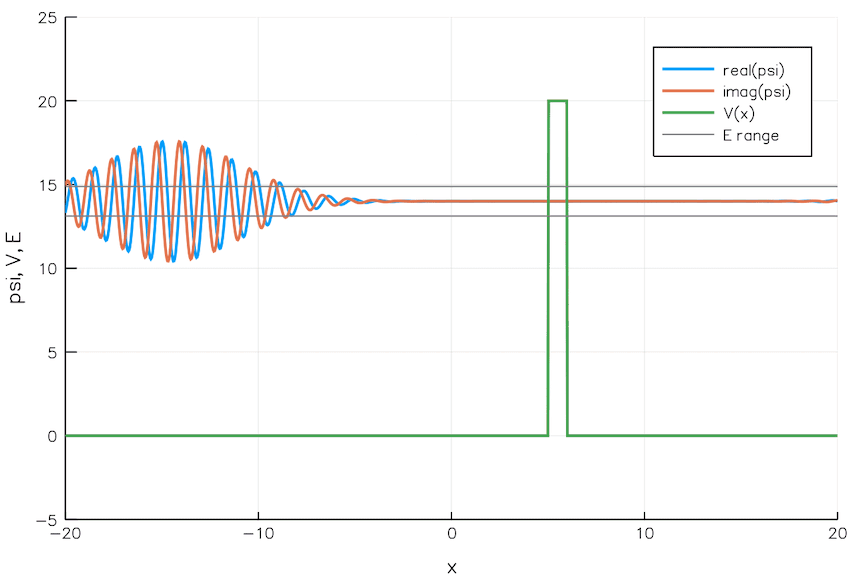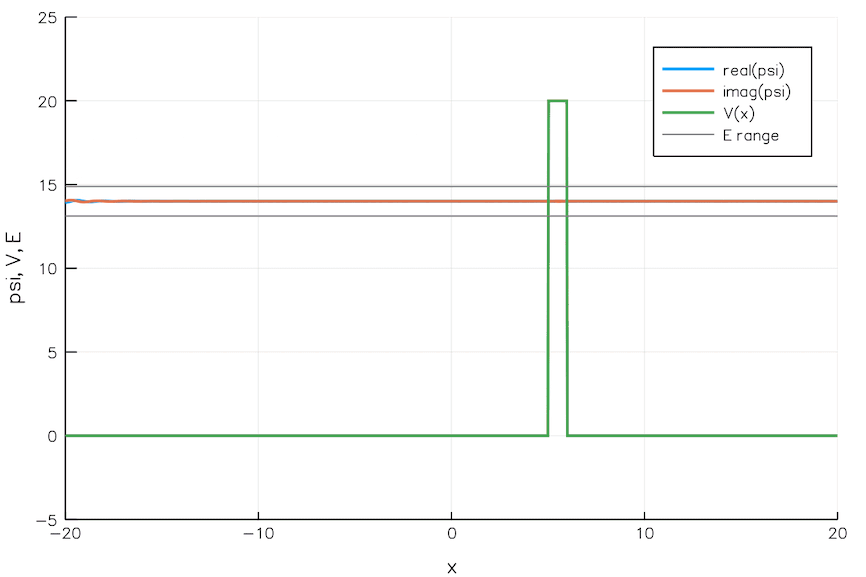

퍼텐셜 장벽에 입사하는 파동 패킷의 시뮬레이션. 상대 단위에서 장벽 에너지는 14인 파동 패킷 평균 에너지보다 큰 20입니다. 파동 패킷의 일부는 장벽을 통과합니다.

파동 함수는 입자들의 물리계에 대해 알 수 있는 모든 것을 명시한다.^[8] 따라서 양자역학의 문제는 계의 파동 함수를 분석한다. 슈뢰딩거 방정식과 같은 수학적 공식을 사용하여 알려진 파동 함수의 시간적 진화를 추론할 수 있다. 이 파동 함수의 절댓값의 제곱은 입자 위치의 확률 분포와 직접적으로 관련이 있으며, 이는 입자가 해당 위치에서 측정될 확률을 설명한다.

애니메이션에서 보이는 바와 같이, 파동 패킷이 장벽에 입사하면 대부분은 반사되고 일부는 장벽을 통과한다. 파동 패킷은 더 비국소화된다. 장벽의 양쪽에 있으며 최대 진폭은 낮아졌지만 적분된 제곱 크기는 같다. 즉, 입자가 어딘가에 있을 확률은 여전히 1이다. 장벽이 넓을수록 장벽 에너지가 높을수록 터널링 확률은 낮아진다.

직사각형 장벽과 같이 터널링 장벽의 일부 모델은 대수적으로 분석하고 풀 수 있다.^[9] 대부분의 문제는 대수적 해가 없으므로 수치 해를 사용한다. "반고전적 방법"은 WKB 근사와 같이 계산하기 쉬운 근사 해를 제공한다.

장벽을 통과하는 양자 터널링. 터널링된 입자의 에너지는 같지만 확률 진폭은 감소합니다.

== 슈뢰딩거 방정식 ==

단일 입자의 1차원 시간에 무관한 슈뢰딩거 방정식은 다음과 같이 쓸 수 있다.^[67]

-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \Psi(x) + V(x) \Psi(x) = E \Psi(x)

여기서

$\hbar$ 는 환산 플랑크 상수이다.
''m''은 입자의 질량이다.
''x''는 입자의 운동 방향으로 측정된 거리를 나타낸다.
Ψ는 슈뢰딩거 파동 함수이다.
''V''는 입자의 퍼텐셜 에너지이다(어떤 편리한 기준 레벨을 기준으로 측정).
''E''는 ''x''축 방향의 운동과 관련된 입자의 에너지이다(''V''를 기준으로 측정).

슈뢰딩거 방정식의 해는 V(x) - E 값에 따라 달라진다. V(x) - E 가 상수이고 음수이면, 슈뢰딩거 방정식은 다음과 같은 형태로 쓸 수 있으며,

\frac{d^2}{dx^2} \Psi(x) = -k^2 \Psi(x), \qquad \text{where} \quad k^2=- \frac{2m}{\hbar^2} (V(x) - E).

이 방정식의 해는 위상 상수 +''k'' 또는 −''k''를 갖는 진행파를 나타낸다. V(x) - E 가 상수이고 양수이면 슈뢰딩거 방정식은 다음과 같은 형태로 쓸 수 있다.

\frac{d^2}{dx^2} \Psi(x) = {\kappa}^2 \Psi(x), \qquad \text{where} \quad {\kappa}^2= \frac{2m}{\hbar^2} (V(x) - E).

이 방정식의 해는 에바네슨트파 형태의 증가 및 감소 지수 함수이다. V(x) - E 가 위치에 따라 변하는 경우에도, V(x) - E 가 음수인지 양수인지에 따라 동일한 해의 형태가 결정된다.

파동 함수는 계의 모든 정보를 가지고 있다.^[67]일반적으로 파동 함수는 위치의 함수로 표현되며, 이 경우 파동 함수는 어떤 위치에서 입자를 발견할 확률을 준다(2승 절댓값이 확률 밀도 함수에 대응한다). 장벽을 높이거나 넓게 하는 극한을 취하면 투과 확률은 낮아진다.

직사각형 포텐셜 장벽과 같은 간단한 모형에서는 해석적 해가 존재하지만, 일반적으로 해석적 해를 얻는 것은 어렵다.

== WKB 근사 ==

WKB 근사는 슈뢰딩거 방정식의 근사해를 구하는 방법 중 하나로, 퍼텐셜 변화가 완만할 때 유용하다.^[67] 파동함수를

\Psi(x) = e^{\Phi(x)}

형태로 나타내고,

\Phi'(x)

를 실수부와 허수부로 분리하여^[67] 반고전 근사를 이용하면, 슈뢰딩거 방정식은 해밀턴-야코비 방정식으로 귀착된다.^[67]

고전적인 운동의 경우와 터널링의 경우, 두가지 극단적인 경우에 대해서 해를 구하면 다음과 같다.

고전적인 운동의 경우:

::

\Psi(x) \approx C \frac{ e^{i \int dx \sqrt{\frac{2m}{\hbar^2} \left( E - V(x) \right)} + \theta} }{\sqrt[4]{\frac{2m}{\hbar^2} \left( E - V(x) \right)}}

터널링의 경우:

::

\Psi(x) \approx \frac{ C_{+} e^{+\int dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}} + C_{-} e^{-\int dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}}{\sqrt[4]{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}

두 경우 모두에서, 고전적 전환점

E = V(x)

근처에서는 근사해가 유효하지 않다.^[67] 이러한 문제를 해결하기 위해, 고전적 전환점 근처에서는 에어리 함수를 이용하여 해를 구하고, 이를 통해 전 영역에서 유효한 근사해를 얻을 수 있다.^[67]

WKB 근사를 이용하면 터널링 확률을 다음과 같이 근사적으로 계산할 수 있다.^[67]

:

T(E) = e^{-2\int_{x_1}^{x_2} dx \sqrt{\frac{2m}{\hbar^2} \left[ V(x) - E \right]}}

위 식에서

x_1

과

x_2

는 고전적으로 입자가 되돌아오는 지점, 즉 퍼텐셜 에너지와 입자의 에너지가 같아지는 지점을 의미한다. 직사각형 장벽의 경우, 위 식은 다음과 같이 단순화된다.

:

T(E) = e^{-2\sqrt{\frac{2m}{\hbar^2}(V_0-E)}(x_2-x_1)}

3. 1. 슈뢰딩거 방정식

단일 입자의 1차원 시간에 무관한 슈뢰딩거 방정식은 다음과 같이 쓸 수 있다.^[67]

-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \Psi(x) + V(x) \Psi(x) = E \Psi(x)

여기서

$\hbar$ 는 환산 플랑크 상수이다.
''m''은 입자의 질량이다.
''x''는 입자의 운동 방향으로 측정된 거리를 나타낸다.
Ψ는 슈뢰딩거 파동 함수이다.
''V''는 입자의 퍼텐셜 에너지이다(어떤 편리한 기준 레벨을 기준으로 측정).
''E''는 ''x''축 방향의 운동과 관련된 입자의 에너지이다(''V''를 기준으로 측정).

슈뢰딩거 방정식의 해는 V(x) - E 값에 따라 달라진다. V(x) - E 가 상수이고 음수이면, 슈뢰딩거 방정식은 다음과 같은 형태로 쓸 수 있으며,

\frac{d^2}{dx^2} \Psi(x) =  -k^2 \Psi(x), \qquad \text{where} \quad k^2=- \frac{2m}{\hbar^2} (V(x) - E).

이 방정식의 해는 위상 상수 +''k'' 또는 −''k''를 갖는 진행파를 나타낸다. V(x) - E 가 상수이고 양수이면 슈뢰딩거 방정식은 다음과 같은 형태로 쓸 수 있다.

\frac{d^2}{dx^2} \Psi(x) =  {\kappa}^2 \Psi(x), \qquad \text{where} \quad {\kappa}^2= \frac{2m}{\hbar^2} (V(x) - E).

이 방정식의 해는 에바네슨트파 형태의 증가 및 감소 지수 함수이다. V(x) - E 가 위치에 따라 변하는 경우에도, V(x) - E 가 음수인지 양수인지에 따라 동일한 해의 형태가 결정된다.

파동 함수는 계의 모든 정보를 가지고 있다.^[67]일반적으로 파동 함수는 위치의 함수로 표현되며, 이 경우 파동 함수는 어떤 위치에서 입자를 발견할 확률을 준다(2승 절댓값이 확률 밀도 함수에 대응한다). 장벽을 높이거나 넓게 하는 극한을 취하면 투과 확률은 낮아진다.

직사각형 포텐셜 장벽과 같은 간단한 모형에서는 해석적 해가 존재하지만, 일반적으로 해석적 해를 얻는 것은 어렵다.

3. 2. WKB 근사

WKB 근사는 슈뢰딩거 방정식의 근사해를 구하는 방법 중 하나로, 퍼텐셜 변화가 완만할 때 유용하다.^[67] 파동함수를

\Psi(x) = e^{\Phi(x)}

형태로 나타내고,

\Phi'(x)

를 실수부와 허수부로 분리하여^[67] 반고전 근사를 이용하면, 슈뢰딩거 방정식은 해밀턴-야코비 방정식으로 귀착된다.^[67]

고전적인 운동의 경우와 터널링의 경우, 두가지 극단적인 경우에 대해서 해를 구하면 다음과 같다.

고전적인 운동의 경우:

::

\Psi(x) \approx C \frac{ e^{i \int dx \sqrt{\frac{2m}{\hbar^2} \left( E - V(x) \right)} + \theta} }{\sqrt[4]{\frac{2m}{\hbar^2} \left( E - V(x) \right)}}

터널링의 경우:

::

\Psi(x) \approx \frac{ C_{+} e^{+\int dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}} + C_{-} e^{-\int dx \sqrt{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}}{\sqrt[4]{\frac{2m}{\hbar^2} \left( V(x) - E \right)}}

두 경우 모두에서, 고전적 전환점

E = V(x)

근처에서는 근사해가 유효하지 않다.^[67] 이러한 문제를 해결하기 위해, 고전적 전환점 근처에서는 에어리 함수를 이용하여 해를 구하고, 이를 통해 전 영역에서 유효한 근사해를 얻을 수 있다.^[67]

WKB 근사를 이용하면 터널링 확률을 다음과 같이 근사적으로 계산할 수 있다.^[67]

:

T(E) = e^{-2\int_{x_1}^{x_2} dx \sqrt{\frac{2m}{\hbar^2} \left[ V(x) - E \right]}}

위 식에서

x_1

과

x_2

는 고전적으로 입자가 되돌아오는 지점, 즉 퍼텐셜 에너지와 입자의 에너지가 같아지는 지점을 의미한다. 직사각형 장벽의 경우, 위 식은 다음과 같이 단순화된다.

:

T(E) = e^{-2\sqrt{\frac{2m}{\hbar^2}(V_0-E)}(x_2-x_1)}

4. 응용 분야

터널링은 몇몇 중요한 거시적 물리 현상의 원인이다.

터널링은 초고밀도 집적회로(VLSI) 전자 장치에서 누설 전류의 원인이 되며, 이는 상당한 전력 소모와 발열 효과를 초래하여 이러한 장치에 문제를 일으킨다. 이는 마이크로 전자 장치 요소의 소형화 한계로 간주된다.^[20] 터널링은 플래시 메모리의 플로팅 게이트를 프로그래밍하는 데 사용되는 기본적인 기술이다.

전자의 냉방출(cold emission)은 반도체 및 초전도체 물리학과 관련이 있다. 이는 열전자 방출과 유사하며, 전기장이 매우 클 때, 장벽이 충분히 얇아져 전자가 원자 상태에서 터널링을 통해 밖으로 나올 수 있으며, 이는 전기장에 따라 거의 지수적으로 변하는 전류를 발생시킨다.^[21] 이러한 재료는 플래시 메모리, 진공관 및 일부 전자 현미경에 중요하다.

매우 얇은 절연체로 두 개의 도체를 분리하여 간단한 장벽을 만들 수 있는데, 이것이 터널 접합이다.^[22] 조셉슨 접합은 양자 터널링과 초전도성을 이용하여 조셉슨 효과를 생성한다. 이것은 전압과 자기장의 정밀 측정^[21]뿐만 아니라 다중 접합 태양 전지에도 응용된다.

다이오드는 한 방향으로의 전류 흐름을 다른 방향보다 더 잘 허용하는 전기적 반도체 소자이다. 이 소자는 그 목적을 달성하기 위해 N형 반도체와 P형 반도체 사이의 공핍층에 의존한다. 이들이 강하게 도핑될 때 공핍층은 터널링이 가능할 만큼 충분히 얇아질 수 있다. 작은 순방향 바이어스가 인가되면 터널링으로 인한 전류가 상당해진다. 이것은 p형과 n형 전도대의 에너지 준위가 같아지는 전압 바이어스 지점에서 최대값을 갖는다. 전압 바이어스가 증가함에 따라 두 전도대가 더 이상 정렬되지 않고 다이오드는 일반적으로 작동한다.^[23]

터널링 전류가 급격히 감소하기 때문에 전압이 증가함에 따라 전류가 감소하는 전압 범위를 갖는 터널 다이오드를 만들 수 있다. 이러한 특이한 특성은 바이어스 전압만큼 빠르게 특성 터널링 확률이 변하는 고속 장치와 같은 일부 응용 분야에 사용된다.^[23]

공명 터널 다이오드는 유사한 결과를 얻기 위해 매우 다른 방식으로 양자 터널링을 이용한다. 이 다이오드는 특정 전압을 선호하는 전류를 갖는 공명 전압을 가지며, 높은 에너지 전도대를 가진 두 개의 얇은 층을 서로 가깝게 배치하여 달성된다. 이것은 이산적인 최저 에너지 준위를 갖는 양자 퍼텐셜 우물을 생성한다. 이 에너지 준위가 전자의 에너지 준위보다 높으면 터널링이 발생하지 않고 다이오드는 역 바이어스 상태가 된다. 두 전압 에너지가 정렬되면 전자는 열린 와이어처럼 흐른다. 전압이 더 증가함에 따라 터널링은 불가능해지고 다이오드는 두 번째 에너지 준위가 눈에 띄기 전에 다시 일반 다이오드처럼 작동한다.^[24]

유럽의 한 연구 프로젝트에서 게이트(채널)를 열적 주입이 아닌 양자 터널링을 통해 제어하는 전계 효과 트랜지스터를 시연하여, 게이트 전압을 약 1볼트에서 0.2볼트로 줄이고 전력 소비량을 최대 100배까지 줄였습니다. 이러한 트랜지스터를 VLSI 칩으로 확장할 수 있다면 집적 회로의 전력당 성능을 향상시킬 수 있을 것입니다.^[25]^[26]

드루드-로렌츠 모형은 금속 내에서 전자의 전도 현상을 잘 예측하지만, 전자의 충돌 현상을 설명하기 위해서는 양자 터널링을 이용하는 것이 더욱 효과적이다.^[21] 자유 전자 파동 패킷이 균일하게 간격을 둔 퍼텐셜 장벽의 긴 배열을 만나면, 반사된 파동 패킷이 모든 장벽 사이에서 투과된 파동 패킷과 균일하게 간섭하여 100% 투과가 가능해진다. 이 이론은 양전하를 띤 원자핵이 완벽하게 직사각형 배열을 이루면 전자가 자유 전자로서 금속을 통과하여 매우 높은 전기 전도도를 나타내고, 금속 내 불순물이 이를 방해한다고 예측한다.^[21]

게르트 비니히와 하인리히 로러가 발명한 주사 터널링 현미경(STM)은 물질 표면의 개별 원자를 이미징할 수 있게 해준다.^[21] 이것은 거리에 따른 양자 터널링의 관계를 이용하여 작동한다. STM의 침 끝을 전압 바이어스가 걸린 전도성 표면에 가까이 가져가면, 침과 표면 사이에서 터널링되는 전자의 전류를 측정하여 침과 표면 사이의 거리를 알 수 있다. 전압이 인가되면 크기가 변하는 압전소자를 사용하여 침의 높이를 조절하여 터널링 전류를 일정하게 유지할 수 있다. 이러한 막대에 인가되는 시간에 따라 변하는 전압을 기록하여 전도체 표면의 영상을 얻을 수 있다.^[21] STM은 0.001 nm의 정확도를 가지며, 이는 원자 지름의 약 1%에 해당한다.^[24]

양자 터널링은 핵융합에 필수적인 현상이다. 항성핵의 온도는 일반적으로 원자핵이 쿨롱 장벽을 극복하고 열핵융합을 달성하기에 충분하지 않다. 양자 터널링은 이 장벽을 통과할 확률을 높인다. 이 확률은 여전히 낮지만, 항성핵에 있는 엄청난 수의 핵은 꾸준한 융합 반응을 유지하기에 충분하다.^[27]

방사성 붕괴는 불안정한 원자핵이 안정된 생성물을 형성하기 위해 입자와 에너지를 방출하는 과정이다. 이는 입자가 핵에서 터널링을 통해 방출되는 방식으로 이루어진다(핵으로 터널링하는 전자는 전자 포획이다). 이는 양자 터널링의 최초 응용 사례였다. 방사성 붕괴는 우주생물학에서 중요한 문제인데, 이 양자 터널링의 결과로 인해 태양 복사가 불가능하거나 효과적이지 않은 항성 주변 생명체 거주 가능 영역 외부 환경(지하 해양)에 대해 긴 시간 간격에 걸쳐 일정한 에너지원이 생성되기 때문이다.^[27]

양자 터널링은 가설적인 양성자 붕괴의 메커니즘 중 하나일 수 있다.^[28]^[29]

성간물질에서 일어나는 화학 반응은 매우 낮은 에너지에서 발생합니다. 아마도 가장 기본적인 이온-분자 반응은 수소 이온과 수소 분자를 포함할 것입니다.

수소 동위원소인 중수소를 사용하는 동일한 반응에 대한 양자 역학적 터널링 비율, D^- + H₂ → H^- + HD는 이온 트랩에서 실험적으로 측정되었습니다. 중수소는 이온 트랩에 넣어 냉각되었습니다. 그런 다음 트랩에 수소를 채웠습니다. 실험에 사용된 온도에서 반응에 대한 에너지 장벽은 고전 역학만으로는 반응이 성공하는 것을 허용하지 않았습니다. 양자 터널링을 통해 드문 충돌에서 반응이 일어날 수 있었습니다. 실험 데이터를 통해 계산된 결과, 1000억 번의 충돌 중 한 번꼴로 반응이 일어났습니다.^[30]

화학 반응 속도론에서, 원소의 가벼운 동위원소를 더 무거운 동위원소로 치환하면 일반적으로 반응 속도가 느려집니다. 이는 일반적으로 가볍고 무거운 동위원소를 포함하는 화학 결합의 영점 진동 에너지 차이에 기인하며, 일반적으로 전이 상태 이론을 사용하여 모델링됩니다. 그러나 특정 경우에는 반고전적 처리로는 설명할 수 없는 큰 동위원소 효과가 관찰되며, 양자 터널링이 필요합니다. R. P. Bell은 이 현상을 모델링하는 데 일반적으로 사용되는 아레니우스 반응 속도론의 수정된 처리 방식을 개발했습니다.^[31]

양자 터널링 효과를 고려하면 성간운에서 다양한 분자들의 천체화학적 합성을 설명할 수 있습니다. 예를 들어 분자 수소, 물(얼음), 그리고 생명의 기원에 중요한 포름알데히드의 합성을 설명할 수 있습니다.^[27] 분자 수소의 터널링 현상은 실험실에서 관측되었습니다.^[32]

양자 터널링은 양자 생물학에서 중심적인 비자명적인 양자 효과 중 하나이다.^[33] 여기서 전자 터널링과 양성자 터널링 모두 중요하다. 전자 터널링은 많은 생화학적 산화 환원 반응(광합성, 세포 호흡)뿐만 아니라 효소 촉매 작용에도 중요한 요소이다. 양성자 터널링은 자발적인 DNA 돌연변이에 중요한 요소이다.^[27]

자발적 돌연변이는 특히 중요한 양성자가 터널링을 한 후 정상적인 DNA 복제가 일어날 때 발생한다.^[34] 수소 결합은 DNA 염기쌍을 연결한다. 수소 결합을 따라 이중 우물 퍼텐셜이 퍼텐셜 에너지 장벽을 분리한다. 이중 우물 퍼텐셜은 비대칭적이어서 한 우물이 다른 우물보다 더 깊어 양성자가 일반적으로 더 깊은 우물에 위치하는 것으로 여겨진다. 돌연변이가 발생하려면 양성자가 얕은 우물로 터널링해야 한다. 양성자의 정상 위치에서의 이동을 토토머 전이라고 한다. DNA 복제가 이 상태에서 일어나면 DNA의 염기쌍 규칙이 위험해져 돌연변이를 일으킬 수 있다.^[35] 페르-올로브뢰딘(Per-Olov Löwdin)은 이중 나선 내에서 자발적 돌연변이의 이론을 처음으로 개발한 사람이다. 생물학에서 양자 터널링으로 유발된 돌연변이의 다른 사례는 노화와 암의 원인으로 여겨진다.^[36]

양자 터널링은 장벽의 두께가 약 1-3 nm 이하일 때 발생하지만,^[73] 이는 몇 가지 중요한 거시적 물리 현상의 원인이 된다. 예를 들어, VLSI에서 전력 손실 및 발열의 원인이 되고, 나아가 컴퓨터 칩의 크기 축소 한계를 결정하는 누설 전류의 원인은 양자 터널링이다.^[74]

4. 1. 주사 터널링 현미경 (STM)

주사 터널링 현미경(STM)은 뾰족한 탐침(팁)을 시료 표면에 접근시켜 시료와 팁 사이에 흐르는 터널 전류를 검출하여 화상 처리하는 방식으로, 물질 표면의 원자 수준 구조를 관찰하는 장비이다.^[21]^[91] STM은 전자의 양자역학적 터널링을 이용한다. 전도성 팁을 시료 표면에 아주 가깝게 가져간 상태에서 팁과 시료 사이에 바이어스 전압을 걸어주면 전자가 진공의 에너지 장벽을 꿰뚫고 한 쪽에서 다른 쪽으로 넘어갈 수 있다.^[21]

게르트 비니히와 하인리히 로러가 발명한 STM은 양자 터널링 확률이 위치에 따라 달라지는 성질을 이용한다.^[91] 바이어스 전압을 건 STM 탐침 끝이 도체 표면에 가까워지면 탐침에서 표면으로 전자가 터널링하여 이것을 전류로 측정할 수 있다. 이 전류를 통해 탐침과 표면 사이의 거리를 측정할 수 있다.^[92] 압전소자에 인가하는 전압을 제어하여 탐침이 표면과 일정 거리를 유지하도록 신축시킬 수 있으며, 압전소자에 인가한 전압의 시간 변화를 기록하면 표면의 영상을 얻을 수 있다.^[21]^[92] STM의 정밀도는 0.001 nm, 즉 원자 지름의 1%에 이른다.^[24]^[93]

4. 2. 터널 다이오드

다이오드는 한 방향으로의 전류 흐름을 다른 방향보다 더 잘 허용하는 전기적 반도체 소자이다. 일반적인 다이오드는 N형 반도체와 P형 반도체 사이의 공핍층을 이용하여 동작한다. 그러나 터널 다이오드는 이 공핍층이 매우 얇아 양자 터널링 현상이 발생한다.^[23]^[85]

작은 순방향 바이어스가 인가되면 터널링으로 인한 전류가 발생하며, 이는 p형과 n형 전도대의 에너지 준위가 같아지는 전압 바이어스 지점에서 최대값을 갖는다. 전압 바이어스가 증가함에 따라 두 전도대가 더 이상 정렬되지 않고 다이오드는 일반적으로 작동한다.^[23]^[85]

터널링 전류가 급격히 감소하기 때문에, 전압이 증가함에 따라 전류가 감소하는 전압 범위를 갖는 터널 다이오드를 만들 수 있다. 이러한 특성은 고속 장치와 같은 일부 응용 분야에 사용된다.^[23]^[86]

공명 터널 다이오드는 매우 다른 방식으로 양자 터널링을 이용한다. 이 다이오드는 특정 전압을 선호하는 전류를 갖는 공명 전압을 가지며, 높은 에너지 전도대를 가진 두 개의 얇은 층을 서로 가깝게 배치하여 달성된다. 이것은 이산적인 최저 에너지 준위를 갖는 양자 퍼텐셜 우물을 생성한다. 이 에너지 준위와 전자의 에너지 준위가 정렬되면 전자는 열린 와이어처럼 흐른다. 전압이 더 증가함에 따라 터널링은 불가능해지고 다이오드는 두 번째 에너지 준위가 눈에 띄기 전에 다시 일반 다이오드처럼 작동한다.^[24]^[87]

4. 3. 핵융합

양자 터널링은 핵융합에 필수적인 현상이다.^[27] 항성핵의 온도는 일반적으로 원자핵이 쿨롱 장벽을 극복하고 열핵융합을 달성하기에 충분하지 않다. 양자 터널링은 이 장벽을 통과할 확률을 높인다.^[27] 이 확률은 여전히 낮지만, 항성핵에 있는 엄청난 수의 핵은 꾸준한 융합 반응을 유지하기에 충분하다.^[27] 항성 내부의 핵융합에도 양자 터널링은 중요하다. 항성 중심부의 온도와 압력으로도 쿨롱 장벽을 넘어 열핵융합을 일으키기에는 충분하지 않다. 그러나 양자 터널링 덕분에 쿨롱 장벽을 통과할 확률이 존재한다.^[75] 이 확률은 매우 낮지만, 항성에 존재하는 원자핵의 수는 막대하여 수십억 년에 걸쳐 꾸준히 핵융합이 지속된다. 이는 곧 생물이 제한된 거주가능 영역에서 진화할 수 있는 전제 조건이 된다.^[75]

4. 4. 양자 생물학

양자 터널링은 양자 생물학에서 중요한 현상이다.^[33] 전자 터널링은 여러 생화학적 산화 환원 반응(광합성, 세포 호흡) 및 효소 촉매 작용에 중요하며, 양성자 터널링은 DNA 자발적 돌연변이에 중요한 역할을 한다.^[27]^[78]

DNA 자발적 돌연변이는 일반적인 DNA 복제 과정에서 양성자가 터널링을 하면서 발생한다.^[34]^[79] DNA 염기쌍은 수소 결합으로 연결되며, 수소 결합을 따라 이중 우물 퍼텐셜이 형성된다. 이중 우물 퍼텐셜은 비대칭적이어서 양성자는 보통 더 깊은 우물에 위치한다. 돌연변이가 발생하려면 양성자가 얕은 우물로 터널링해야 하며, 이 현상을 토토머 전이라고 한다.^[35]^[80] 이 상태에서 DNA 복제가 일어나면 염기쌍 규칙이 깨져 돌연변이가 발생할 수 있다.^[35]^[80] 페르-올로브뢰딘(Per-Olov Löwdin)은 이중 나선 내에서의 자발적 돌연변이 이론을 처음으로 개발했다.^[36] 양자 터널링으로 인한 돌연변이는 노화와 암의 원인으로도 여겨진다.^[36]^[81]

4. 5. 기타 응용

터널링은 초고밀도 집적회로(VLSI) 전자 장치에서 누설 전류의 원인이 되며, 이는 상당한 전력 소모와 발열 효과를 초래한다. 이는 마이크로 전자 장치 요소의 소형화 한계로 간주된다.^[20] 터널링은 플래시 메모리의 플로팅 게이트를 프로그래밍하는 데 사용되는 기본적인 기술이다.

전자의 냉방출(cold emission)은 반도체 및 초전도체 물리학과 관련이 있다. 이는 열전자 방출과 유사하며, 전기장이 매우 클 때, 장벽이 충분히 얇아져 전자가 원자 상태에서 터널링을 통해 밖으로 나올 수 있으며, 이는 전기장에 따라 거의 지수적으로 변하는 전류를 발생시킨다.^[21] 이러한 재료는 플래시 메모리, 진공관 및 일부 전자 현미경에 중요하다.^[82]

매우 얇은 절연체로 두 개의 도체를 분리하여 간단한 장벽을 만들 수 있는데, 이것이 터널 접합이다.^[22] 조셉슨 접합은 양자 터널링과 초전도성을 이용하여 조셉슨 효과를 생성한다. 이것은 전압과 자기장의 정밀 측정^[21]뿐만 아니라 다중 접합 태양 전지에도 응용된다.

유럽의 한 연구 프로젝트에서 게이트(채널)를 열적 주입이 아닌 양자 터널링을 통해 제어하는 전계 효과 트랜지스터를 시연하여, 게이트 전압을 약 1볼트에서 0.2볼트로 줄이고 전력 소비량을 최대 100배까지 줄였다.^[25]^[26] 이러한 트랜지스터를 VLSI 칩으로 확장할 수 있다면 집적 회로의 전력당 성능을 향상시킬 수 있을 것이다.^[88]

5. 관련 현상

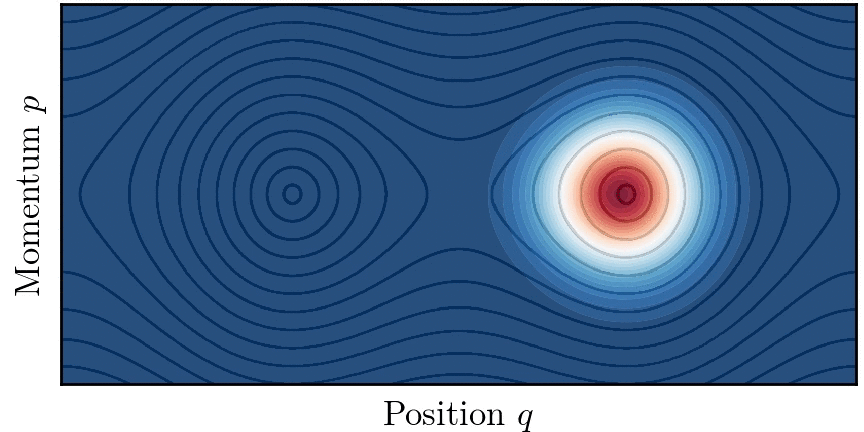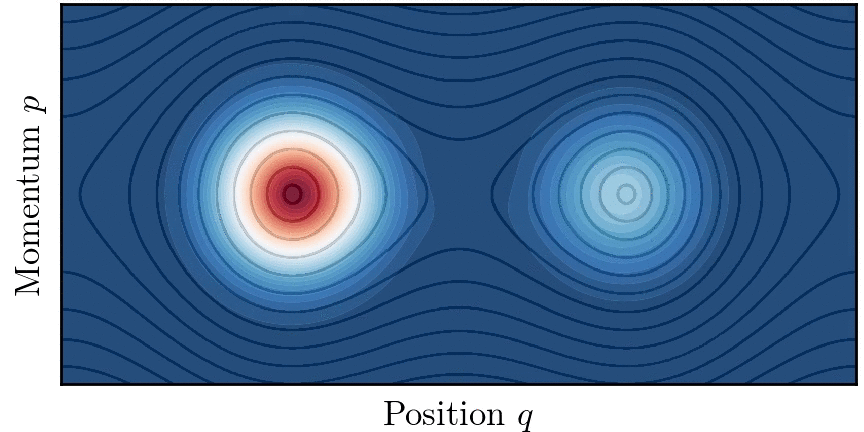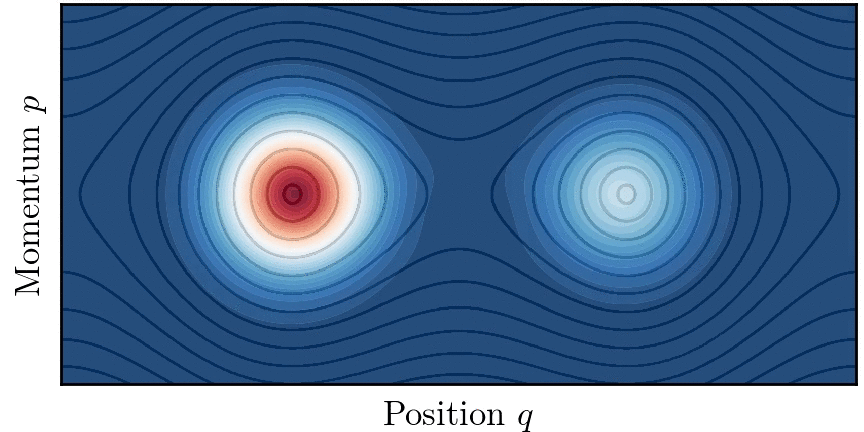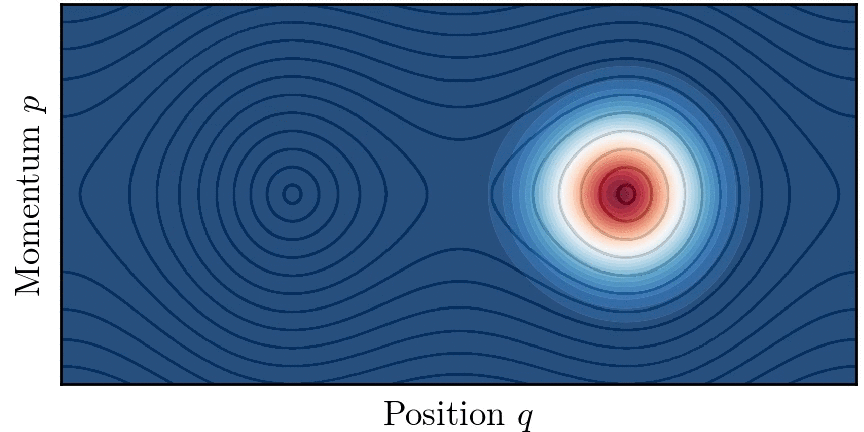
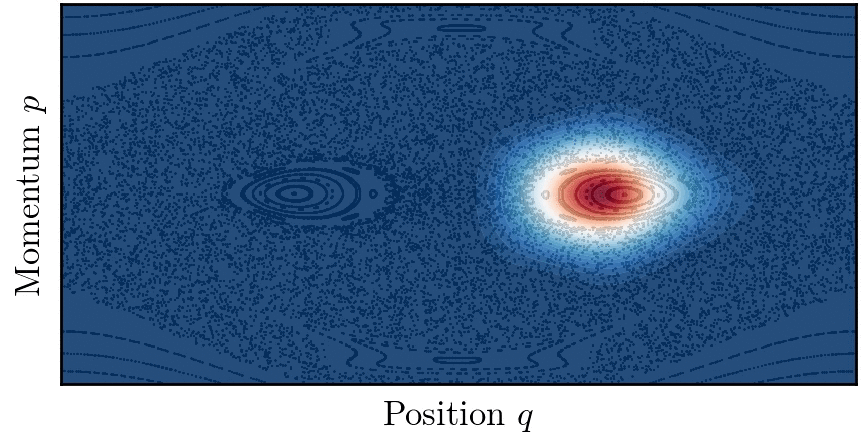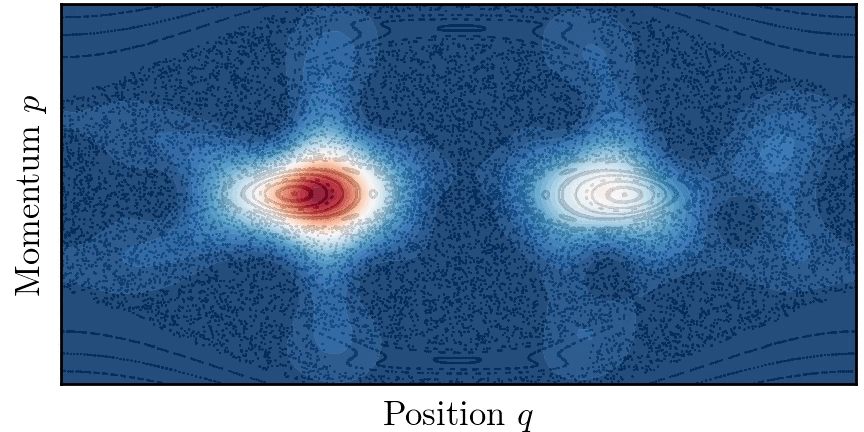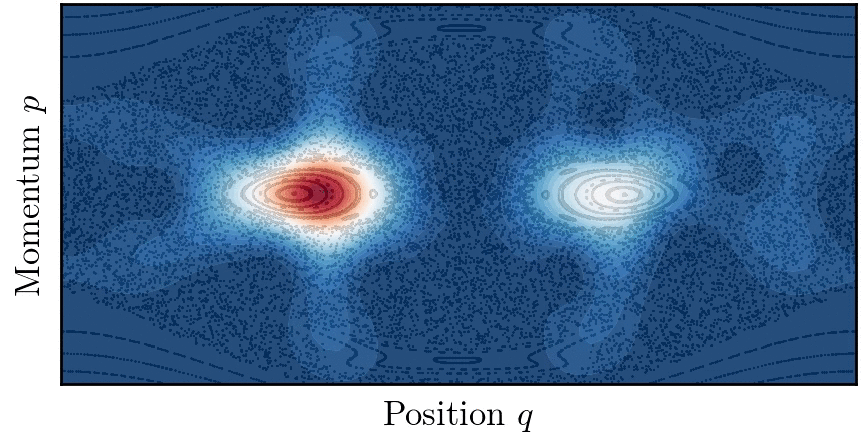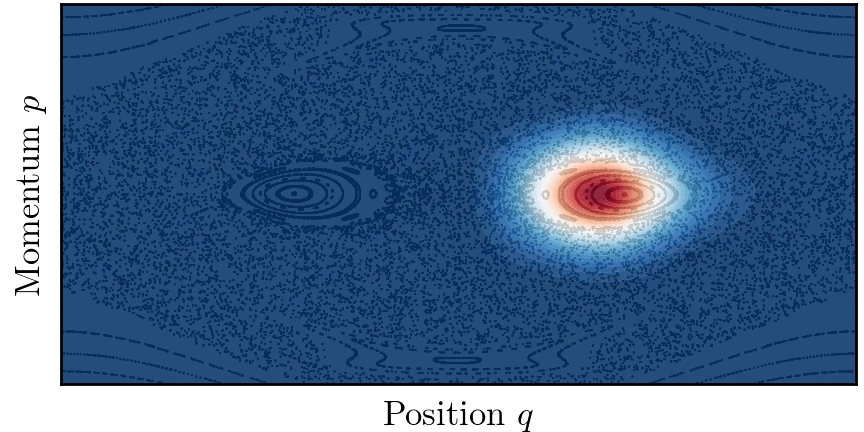
위상 공간에서 보이는 퍼텐셜의 적분 가능한 이중 우물에서의 확률의 양자 터널링 진동

혼돈 보조 터널링: 상호 작용하는 혼돈 영역에 둘러싸인 두 개의 규칙적인 토러스 사이의 진동을 위상 공간에서 보여줌

양자 터널링 개념은 퍼텐셜 장벽이 없더라도 고전적으로 연결되지 않은 영역 사이에 양자 수송이 존재하는 상황으로 확장될 수 있다. 이 현상을 동역학적 터널링(Dynamical tunnelling)이라고 한다.^[44]^[45]

동역학적 터널링 개념은 특히 고차원(d>1)에서의 양자 터널링 문제를 해결하는 데 적합하다. 가적계의 경우, 경계가 있는 고전적인 궤적이 위상 공간의 토리에 국한되는 경우, 터널링은 두 개의 구별되지만 대칭적인 토리 위에 구축된 반고전적인 상태 간의 양자 수송으로 이해될 수 있다.^[46]

실제로 대부분의 시스템은 적분 가능하지 않고 다양한 정도의 혼돈을 보인다. 고전 역학은 혼합된 것으로 여겨지며 시스템 위상 공간은 일반적으로 넓은 혼돈 궤도의 바다로 둘러싸인 규칙적인 궤도의 섬들로 구성된다. 두 개의 대칭적인 토러스 사이에서 수송이 고전적으로 허용되는 혼돈의 바다 존재는 이들 사이의 양자 터널링을 돕는다. 이 현상을 혼돈 보조 터널링이라고 하며,^[47] 시스템 매개변수를 변경할 때 터널링 속도의 급격한 공명을 특징으로 한다.

\hbar

가 일반적인 섬의 크기에 비해 작을 때, 고전적 위상 공간의 미세 구조가 터널링에 중요한 역할을 한다. 특히 두 개의 대칭적인 토러스는 두 섬을 둘러싸는 비선형 공명을 가로지르는 일련의 고전적으로 금지된 전이를 통해 결합된다.^[48]

여러 현상들이 양자 터널링과 같은 거동을 보인다. 대표적인 예로 에바네센트파 결합^[49](빛에 대한 맥스웰 방정식 적용)과 음향학에서 현에 발생하는 파동에 대한 비확산 파동 방정식 적용이 있다. 에바네센트파 결합은 빛이 굴절률이 다른 두 매질 사이의 경계면에서 전반사될 때, 얇은 틈을 통해 빛이 투과하는 현상이다.

이러한 효과들은 직사각형 포텐셜 장벽과 유사하게 모델링된다. 이러한 경우, 파동이 전파되는 전파 매질이 전체적으로 동일하거나 거의 동일하며, 파동이 다르게 전파되는 두 번째 매질이 있다. 이것은 매질 A의 두 영역 사이에 얇은 매질 B 영역으로 설명될 수 있다. 슈뢰딩거 방정식을 이용한 직사각형 장벽의 분석은 파동 방정식이 매질 A에서는 진행파 해를 가지지만 매질 B에서는 실수 지수 해를 갖는다는 조건 하에 이러한 다른 효과에도 적용될 수 있다.

광학에서 매질 A는 진공이고 매질 B는 유리이다. 음향학에서 매질 A는 액체 또는 기체일 수 있고 매질 B는 고체일 수 있다. 두 경우 모두 매질 A는 입자의 전 에너지가 퍼텐셜 에너지보다 큰 영역이고 매질 B는 퍼텐셜 장벽이다. 이것들은 입사파와 그 결과 양방향으로 생성되는 파를 갖는다. 더 많은 매질과 장벽이 있을 수 있으며, 장벽은 불연속일 필요가 없다.

6. 더 알아보기

참조

_[1] 서적 Encyclopedia of Physics https://archive.org/[...] VCH
_[2] 학술지 Quantum mechanics and the equivalence principle 2004-05-06
_[3] 웹사이트 Particle in a Finite Box and Tunneling https://chem.librete[...] 2019-12-05
_[4] 서적 College Physics Brooks/Cole
_[5] 서적 Modern Physics for Scientists and Engineers Prentice Hall
_[6] 뉴스 Quantum Effects At 7/5nm And Beyond https://semiengineer[...] 2018-07-15
_[7] 서적 Quantum Theory of Tunneling https://archive.org/[...] World Scientific
_[8] 서적 Relativistic quantum mechanics McGraw Hill 1964
_[9] 서적 Quantum Mechanics https://archive.org/[...] North Holland, John Wiley & Sons 1966
_[10] 학술지 The Early History of Quantum Tunneling https://physicstoday[...] 2002-08
_[11] 학술지 Zur Theorie der Schrödingerschen Gleichung
_[12] 학술지 Quantum Mechanics and Radioactive Disintegration
_[13] 학술지 Quantum Mechanics and Radioactive Disintegration
_[14] 인터뷰 Hans Bethe – Session I https://www.aip.org/[...] 1966-10-27
_[15] 서적 Nuclear and Radiochemistry https://archive.org/[...] John Wiley & Sons
_[16] 학술지 The forefather (about Leonid Isaakovich Mandelstam)
_[17] 학술지 Long Journey into Tunneling https://www.science.[...] 1974-03-22
_[18] 서적 Nobel laureates and twentieth-century physics http://archive.org/d[...] Cambridge, UK ; New York : Cambridge University Press 2004
_[19] 학술지 Scanning tunneling microscopy—from birth to adolescence 1987-07
_[20] 웹사이트 Applications of ''tunneling'' http://psi.phys.wits[...]
_[21] 서적 Modern Physics for Scientists and Engineers Prentice Hall
_[22] 서적 Encyclopedia of Physics https://archive.org/[...] VCH
_[23] 서적 Modern Physics https://archive.org/[...] John Wiley and Sons
_[24] 서적 Physics for Scientists and Engineers: With Modern Physics Pearson Education
_[25] 학술지 Tunnel field-effect transistors as energy-efficient electronic switches
_[26] 학술지 Theoretical simulation of negative differential transconductance in lateral quantum well nMOS devices https://aip.scitatio[...] 2017-01-23
_[27] 학술지 Quantum tunnelling to the origin and evolution of life
_[28] 학술지 Time-dependent properties of proton decay from crossing single-particle metastable states in deformed nuclei
_[29] 웹사이트 adsabs.harvard.edu http://adsabs.harvar[...]
_[30] 학술지 Tunnelling measured in a very slow ion–molecule reaction https://www.nature.c[...] 2023-03-16
_[31] 서적 The tunnel effect in chemistry Chapman and Hall 1980
_[32] 학술지 Tunnelling measured in a very slow ion–molecule reaction https://www.nature.c[...] 2023-03-01
_[33] 학술지 Quantum Tunnelling to the Origin and Evolution of Life
_[34] 서적 Quantum Biochemistry: Electronic Structure and Biological Activity https://books.google[...] Wiley-VCH
_[35] 서적 Quantum Mechanics: In Physics and Chemistry with Applications to Bioloty https://books.google[...] PHI Learning
_[36] 논문 Roles of Evolution, Quantum Mechanics and Point Mutations in Origins of Cancer 1993-06-01
_[37] 논문 Comments on apparent superluminal propagation 1998
_[38] 논문 Tunneling Confronts Special Relativity 2011
_[39] 웹사이트 Quantum-tunnelling time is measured using ultracold atoms – Physics World https://physicsworld[...] 2020-07-22
_[40] 웹사이트 Quanta Magazine https://www.quantama[...] 2020-10-20
_[41] 논문 Tunneling time, the Hartman effect, and superluminality: A proposed resolution of an old paradox 2006
_[42] 서적 The Dirac Equation https://link.springe[...] 1992
_[43] 논문 Subluminality of relativistic quantum tunneling https://link.aps.org[...] 2023-03-13
_[44] 논문 Quantum dynamical tunneling in bound states https://aip.scitatio[...] 1981-07-01
_[45] 서적 Dynamical Tunneling: Theory and Experiment https://books.google[...] CRC Press 2011-03-09
_[46] 논문 Tunnelling between tori in phase space https://dx.doi.org/1[...] 1986-09-01
_[47] 논문 Chaos-assisted tunneling https://link.aps.org[...] 1994-07-01
_[48] 논문 Resonance-Assisted Tunneling http://www.sciencedi[...] 2002-08-25
_[49] 논문 Time delay of evanescent electromagnetic waves and the analogy to particle tunneling https://link.aps.org[...] 1992-02-01
_[50] 논문 Unpredictable Tunneling of a Classical Wave-Particle Association http://stilton.tnw.u[...] 2009-06-16
_[51] 논문 Hydrodynamic quantum analogs https://iopscience.i[...] 2021-01-01
_[52] 서적 Quantum Theory of Tunneling World Scientific 2003
_[53] 논문 Quantum Mechanics and Radioactive Disintegration https://doi.org/10.1[...] 1929-02-01
_[54] 서적 College Physics Brooks/Cole 2008
_[55] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[56] 웹사이트 The STM (Scanning Tunneling Microscope) [The forgotten contribution of Robert Francis Earhart to the discovery of quantum tunneling.] https://www.research[...] 2016-05-01
_[57] 서적 Zero Time Space Wiley-VCH 2008
_[58] 논문 Quantum Mechanics and Radioactive Disintegration 1928
_[59] 논문 Quantum Mechanics and Radioactive Disintegration 1929
_[60] 인터뷰 Hans Bethe - Session I https://www.aip.org/[...] 1966-10-27
_[61] 서적 Nuclear and Radiochemistry John Wiley & Sons 1964
_[62] 서적 Quantum Theory of Tunneling World Scientific 2003
_[63] 서적 Quantum Theory of Tunneling World Scientific 2003
_[64] 논문 Quantum Tunneling of Water in Beryl: A New State of the Water Molecule http://journals.aps.[...] 2016-04-22
_[65] 논문 Quantum tunneling time http://www.quantum30[...] 2005
_[66] 서적 Zero Time Space Wiley-VCH 2008
_[67] 서적 Relativistic Quantum Mechanics
_[68] 논문 Unpredictable Tunneling of a Classical Wave-Particle Association http://stilton.tnw.u[...] 2009-06-16
_[69] 웹사이트 스핀 편극 공명 터널 효과 발견 https://www.aist.go.[...] 산업기술종합연구소 2002-07-12
_[70] 논문 7pWA-1 강자성 터널 접합의 스핀 편극 공명 터널 효과(터널 자기 저항·스핀 주입 자화 반전, 영역 3) 일반사단법인 일본물리학회 2002
_[71] 논문 磁気トンネル接合の TMR 効果と共鳴トンネル効果 (最近の研究から) https://doi.org/10.1[...] 2003
_[72] 논문 Spin-Polarized Resonant Tunneling in Magnetic Tunnel Junctions https://www.research[...] 2002
_[73] 서적 Encyclopedia of Physics VCH 1991
_[74] 웹사이트 Applications of tunneling http://psi.phys.wits[...] 2006-02-21
_[75] 논문 Quantum tunnelling to the origin and evolution of life https://www.ncbi.nlm[...] 2013
_[76] 논문 Quantum tunnelling to the origin and evolution of life https://www.ncbi.nlm[...] 2013
_[77] 논문 Quantum tunnelling to the origin and evolution of life https://www.ncbi.nlm[...] 2013
_[78] 논문 Quantum tunnelling to the origin and evolution of life https://www.ncbi.nlm[...] 2013
_[79] 서적 Quantum Biochemistry: Electronic Structure and Biological Activity https://books.google[...] Wiley-VCH 2014
_[80] 서적 Quantum Mechanics: In Physics and Chemistry with Applications to Bioloty https://books.google[...] PHI Learning 2011
_[81] 논문 Roles of Evolution, Quantum Mechanics and Point Mutations in Origins of Cancer 1993-06
_[82] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[83] 서적 Encyclopedia of Physics VCH 1991
_[84] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[85] 서적 Modern Physics John Wiley and Sons 1983
_[86] 서적 Modern Physics John Wiley and Sons 1983
_[87] 서적 Physics for Scientists and Engineers: With Modern Physics Pearson Education 2004
_[88] 논문 Tunnel field-effect transistors as energy-efficient electronic switches 2011
_[89] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[90] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[91] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[92] 서적 Modern Physics for Scientists and Engineers Prentice Hall 2004
_[93] 서적 Physics for Scientists and Engineers: With Modern Physics Pearson Education 2004
_[94] 서적 Quantum Theory of Tunneling World Scientific 2003
_[95] 논문 Comments on apparent superluminal propagation 1998
_[96] 논문 Tunneling Confronts Special Relativity 2011
_[97] 웹사이트 Quantum tunneling time http://cosmos.asu.ed[...] 2013-03-08
_[98] 문서 지구의 안정된 궤도 공전
_[99] 서적 우주의 이해 전남대학교출판부 2007
_[100] 논문 Zur Deutung der Molekelspektren III 1927-11
_[101] 논문 Zur Quantentheorie des Atomkernes 1928-03
_[102] 서적 환경에너지 공학 동화기술 2009
_[103] 논문 Wave Mechanics and Radioactive Disintegration http://www.nature.co[...] 1928-09

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com